Inhoud

1. Inleiding
2. Het tegengestelde van een getal
3. Het omgekeerde van een getal

Inleiding

In de wiskunde worden vaak woorden gebruikt waarvan je de (wiskundige) betekenis goed moeten kennen. Anders raak je het spoor bijster en begrijp je er niets meer van. Dit geldt ook voor de begrippen:

• Het tegengestelde van een getal
• Het omgekeerde van een getal

Sommige leerlingen weten echt het verschil tussen beide begrippen niet. Ik ga dat nu even met een paar voorbeelden uitleggen!

Het tegengestelde van een getal

Het tegengestelde van 3 is -3 en het tegengestelde van -5 is 5. Van mijn oude wiskundeleraar heb ik geleerd dat je altijd het tegengestelde van een getal krijgt als je dat getal met -1 vermenigvuldigt.

Voorbeelden:

• Het tegengestelde van 3 is -1 × 3 = -3

• Het tegengestelde van -5 is -1 × -5 = 5

Let op!   Het tegengestelde van 0 blijft gewoon 0 want -0 = 0!

Belangrijke eigenschappen: 

• Als je bij een getal het tegengestelde van dat getal optelt krijg je 0. In formulevorm betekent dat:   a + -a =  0

• Een getal ergens van aftrekken is hetzelfde als het tegengestelde van dat getal erbij optellen. Voorbeeld:   5 - 2 = 5 + -2 = 3

Bij het oplossen van vergelijkingen maken we van deze eigenschappen vaak gebruik. En, neem van mij aan dat het wel erg handig is als je vergelijkingen goed kunt oplossen! Klik maar eens op volgende twee voorbeelden:

• Voorbeeld 1 

• Voorbeeld 2 

Het omgekeerde van een getal

Het omgekeerde van een gewone breuk is het makkelijkst!

Het omgekeerde van

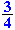is

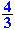. Je verwisselt gewoon teller en noemer. Of anders

gezegd, je zet de breuk op zijn kop.

Maar wat is nu het omgekeerde van 2

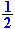? Het handigste is om van 2

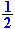eerst

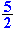te

maken en dan het omgekeerde te nemen. Het omgekeerde van 2

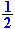is dus

.

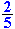Het omgekeerde van 2 vind je door van 2 eerst

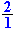te maken en dan het omgekeerde te

nemen. Dat wordt dan

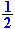. Van mijn goede oude wiskundeleraar heb ik geleerd dat je

altijd het omgekeerde van een getal vindt door

te nemen.

Let op!   Het omgekeerde van 0 kan niet want

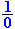bestaat immers niet!

Belangrijke eigenschappen:

• Als je een getal met het omgekeerde van dat getal vermenigvuldigt krijg je 1. In

  formulevorm betekent dat    a ×

  =  1

• Een getal delen door een breuk is hetzelfde als dat getal vermenigvuldigen met

  het omgekeerde van die breuk. Voorbeeld: 5 :

  = 5 ×

  = 10

Bij het oplossen van vergelijkingen maken we vaak van het omgekeerde van getallen gebruik. En, neem van mij aan, het is de moeite waard om je hier even in te verdiepen! Klik maar eens op het volgende voorbeeld:

• Voorbeeld 3 

Als laatste een voorbeeld van een vergelijking waar je zowel het tegengestelde als het omgekeerde nodig hebt.

• Voorbeeld  4